About the maths….it’s quite neat!

…OK, I think I’m having a love-hate relationship with the maths on this course. My brain has finally spun-up memories of calculus from 30+ years ago and I can get going with the assignments questions.

I’m not loving it: integration, differentiation, linear algebra, inner products, probabilities – and hearing the phrase “this is GCSE level” is never reassuring when GCSEs were so long ago.

However, I marvel at how quantum mechanics can be described using maths tools that are well known and well used. Nothing new is required, so far at least (except for a nifty way of abstracting vectors called Dirac notation).

Slowly things are mapping in my brain.

In classic physics a simple formula will do since we have one deterministic value, eg. or .

In quantum we’re dealing with the fact that there are many answers and probabilities associated with observing each one.

So how do you represent those multiple answers and probabilities? Each answer (eigenstate) can be stored in a vector, and a scalar (eigenvalue) associated with it. That scalar is the amplitude of probability, which when squared gives us the actual probability of that eigenstate being the reality (depending on what you call reality, i.e. wave function collapse or many-worlds, or…).

This vector can have discrete eigenstates – for example the superposition of spin-up and spin-down of an electron – or can be continuous – the position of a particle. The more continuous the vector the more it resembles a function returning the eigenvalues. This is the wave function.

That leads us to some beautiful maths.

We can play with these vectors using Dirac notation (bras () and kets (), or as vectors, or as components. Here’s three ways to view the inner product of B and A:

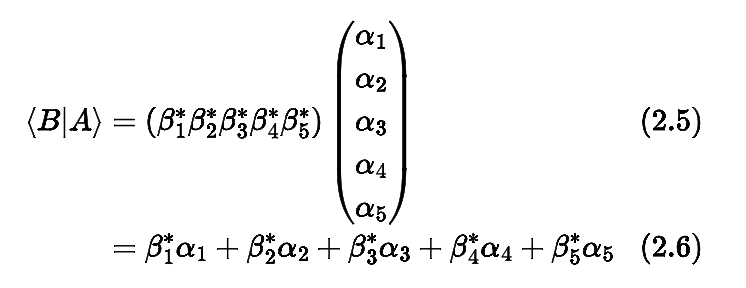
Or when finding the average position of a particle is the result of making the observation many times – which is integration between and of the probability density function multiplied by the position operator (the probability density function is the modulus square of the normalised wave function – something from probability theory and given us by the Born rule).

So, yes, my relationship with maths in quantum physics is a love-hate one…right now it’s on the love side…but, ask me again in a few hours…. 🙂